
I'm not actually going to solve any for you. So those are the four different ways, the pros and cons, and some things to think about when you're solving a problem. So you have to remember the formula, and it can get ugly. It's typically not as easy as some of these other methods, completing the square, I would say, is a little bit easier than that but it's something you have to remember. If you're using square roots, which some people don't always like, you always have to use square roots as well. It's great, again, because you can always use it. It's not always going to be the nicest situation. If you're dealing with a coefficient or an odd middle term or something like that you're going to introduce fractions. But the downfall is that it can get ugly. There will never be a time you won't be able to complete the square. The great thing about completing the square is we can always do it. It actually isn't the case very often at all.Ĭompleting the square. It's great when applicable, but it's not always the case. Any time you have an X term or something like that we're not going to be able to use it. The only problem is that it's not always the situation we're dealing with. So, the pro: is it's great when you're solving for something squared. The next one we're going to talk about is the square root property. Solve the equation x 2 + 6 x 7 0 by factoring. Second case: When b is positive and c is negative. Factor and solve the quadratic equation x 2 + 6 x + 8 0. So fast and easy, but not always applicable. Factoring quadratic equations when the coefficient of x is equal to 1 First case: When b and c are both positive. So it's fast and easy when it's usable, but not always factorable, either. Oftentimes, we're dealing with a quadratic that is not factorable, so then factoring is not going to help us. Factoring is typically the fastest and easiest way of solving something when it's factorable. The 'check' means pros and the 'minus' means cons. So I'm just going to go down the row and talk about each one. We can use these methods at different times, and what I want to do is just talk about when we can use them, why they're good, and why they're bad. We have factoring, square root property, completing the square, and the quadratic formula. So we have four different ways at our convenience.
#FACTORING QUADRATIC EQUATIONS PLUS#
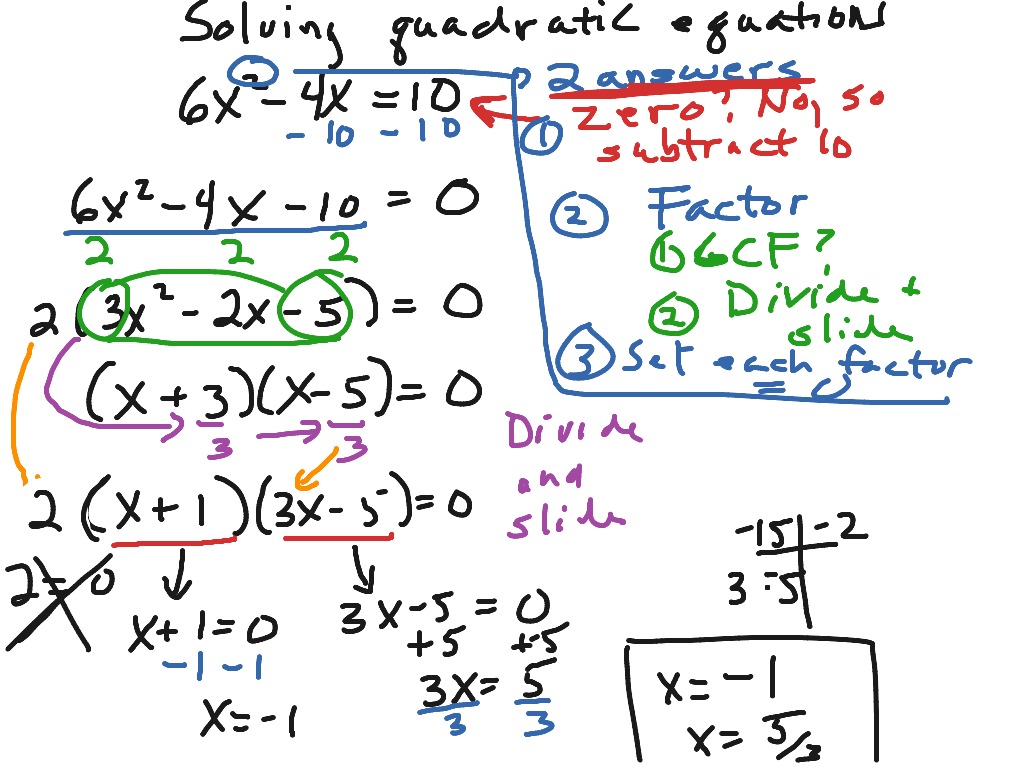
What I mean by that is anything of the form: ax² plus bx plus c. Now we have to divide the two factors +6 and +9 by the coefficient of x 2, that is 2.So what I want to talk about now is an overview of all the different ways of solving a quadratic equation. So, m ultiply the coefficient of x 2 and the constant term "+27".ĭecompose +54 into two factors such that the product of two factors is equal to +54 and the addition of two factors is equal to the coefficient of x, that is +15. In the given quadratic equation, the coefficient of x 2 is not 1. In the given quadratic equation, the coefficient of x 2 is 1.ĭecompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is +9.įactor the given quadratic equation using +2 and +7 and solve for x.ĭecompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is -9.įactor the given quadratic equation using -2 and -7 and solve for x.ĭecompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is +2.įactor the given quadratic equation using +5 and -3 and solve for x.ĭecompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is -2.įactor the given quadratic equation using +3 and -5 and solve for x. (iv) Write the remaining number along with x (This is explained in the following example). (iii) Divide the two factors by the coefficient of x 2 and simplify as much as possible. (ii) The product of the two factors must be equal to "ac" and the addition of two factors must be equal to the coefficient of x, that is "b". (i) In a quadratic equation in the form ax 2 + bx + c = 0, if the leading coefficient is not 1, we have to multiply the coefficient of x 2 and the constant term. Solving Quadratic Equations by Factoring when Leading Coefficient is not 1 - Procedure Positive sign for smaller factor and negative sign for larger factor.


 0 kommentar(er)
0 kommentar(er)
